Un primo approccio al numero
PRESENTAZIONE
Questo contributo si rifà ad alcune mie lezioni – e alle osservazioni che ne sono derivate – sui primi approcci all’aritmetica, tenute per l’insegnamento di Didattica della Matematica del corso di laurea in Scienze della Formazione primaria (Università di Bari, sede distaccata di Lecce). Gli argomenti sono stati da me discussi anche con insegnanti di Scuola dell’Infanzia e Primaria degli Istituti Comprensivi “A. Novelli” di Ancona e “Leonardo da Vinci” di Cavallino (LE).
DUE PRINCIPI BASILARI PER L’ARITMETICA
Come Jean Piaget evidenziò nella prima parte del secolo scorso, all’inizio della scuola primaria i bambini non hanno ancora pienamente acquisito il significato del contare, che è strettamente connesso col Principio di Conservazione delle Quantità discrete, nel senso che un raggruppamento di oggetti è caratterizzato da una “quantità” che non dipende dalla dislocazione spaziale di quelli. Però tale principio ne presuppone uno altrettanto importante e quasi sempre non considerato esplicitamente: il Principio di Indifferenza, secondo cui il conteggio di un gruppo di oggetti, di cui si lasci immutata la posizione, dà sempre lo stesso numero finale, a prescindere dall’ordine in cui gli oggetti vengano via via contati. Questo secondo principio è talmente insito in noi e connaturato con la pratica del contare – che senza di esso non avrebbe senso – che un adulto può non essere indotto a prendere in considerazione il fatto che un bambino ai primi approcci con l’aritmetica possa non esserne consapevole. Invece ciò è confermato da esperienze da noi svolte.
È importante che gli scolari prendano piena consapevolezza del Principio di Indifferenza, affinché l’ultimo numero contato possa essere assunto come caratteristica di un dato gruppo di oggetti; onde questo sia visto come una sorta di “marchio” del gruppo. Ciò consente di confrontare le numerosità di due gruppi, anche in collocazioni diverse – secondo la ben nota consuetudine del contare – facendo riferimento ai “marchi numerici” finali dei due gruppi.
Perciò non basta che un bambino impari correttamente la cantilena dei numeri, sappia recitarla e sappia usarla nei conteggi. È necessario che egli prenda coscienza – attraverso alcune esperienze semplici da gestire, e perciò limitate a casi che impegnino numeri molto piccoli – che contando in vario modo un gruppo di oggetti, senza alterarne la collocazione, il numero finale resta invariato.
Inoltre, poiché un conteggio di quegli oggetti stabilisce per ciascuno di essi una sorta di “denominazione numerica”, questa rimarrà invariata – insieme al marchio, che esprime la denominazione dell’ultimo oggetto contato – anche rispetto a collocazioni spaziali diverse degli oggetti; cosi come il nome proprio dei componenti di un gruppo di persone resta invariato – insieme all’ultimo che sia stato assegnato – a prescindere da dove esse siano a collocate.
Nei primi approcci aritmetici è fondamentale l’uso delle dita, che – in una sorta di psicomotricità digitale – consente di agevolare lo sviluppo delle cognizioni e delle abilità aritmetiche. Ciò a partire già dai tre anni e qualche mese, in cui il bambino si è ormai abituato a indicare la sua età con il pollice, l’indice e il medio di una mano. Però bisognerà portarlo a capire che quelle tre dita, mostrate insieme, non sono soltanto un contrassegno della sua età. Esse esprimono una rappresentazione di carattere analitico, che cambierebbe se venissero mostrati soltanto l’indice e il medio. Onde, per rappresentare il due o il tre (e la stessa cosa varrà poi per numeri più grandi), non importa quali dita si usino; al contrario di ciò che pensavano alcuni bambini prossimi ai sei anni da noi osservati.
I BLOCCHI ARITMETICI MULTIBASE (BAM)
Per agevolare la comprensione della rappresentazione numerica, in un primo momento sarà opportuno usare la “base due”. In tal modo gli alunni potranno realizzare i pezzi fondamentali mostrati qui sotto e altri ancora.
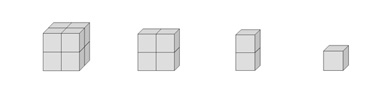
Con quelli – ciascuno usato al più una volta, dato che in “base due”, di norma, due Blocchi vanno aggregati – si possono rappresentare le quantità da 1 a 15. Una volta compresi i concetti in “base due”, si provvederà al loro rinforzo in “base tre” (onde sarà più semplice farli comprendere in “base decimale”). Quindi si passerà alla rappresentazione tramite abaco degli assemblaggi ottenuti tramite i BAM.
Scarica il pdf integrale dell’esperienza.
****
ARTICOLI CORRELATI
– Ali in volo: avvio alla lettura nella scuola per l’infanzia
/didattica-e-apprendimento/ali-volo-avvio-lettura-scuola-l-infanzia-3082853694.shtml
– Avvio alla matematica: blocchi e abachi
/didattica-e-apprendimento/avvio-matematica-blocchi-abachi-403549036.shtml
– Fiammiferi e cifre decimali
/racconti-ed-esperienze/fiammiferi-cifre-decimali-3078923784.shtml
– I ponti di Königsberg e la nascita della teoria dei grafi
/didattica-e-apprendimento/i-ponti-konigsberg-nascita-teoria-grafi-3058592865.shtml
– La matematica salverà l’umanità?
/curricoli-e-saperi/matematica-salvera-l-umanita-405334687.shtml
– Primi passi in aritmetica
/racconti-ed-esperienze/primi-passi-aritmetica-3055506299.shtml
– Saggio e attività – Un uso appropriato e coordinato dei blocchi aritmetici multibase (BAM) e dell’abaco
/speciali/pdf/lenzi4_all.pdf
– Speciale – Matematica: didattica, esperienze, tecnologie
/speciali/pdf/specialemarzo11.pdf
– Verso la conquista del numero
/didattica-e-apprendimento/verso-conquista-numero-4041518306.shtml
Domenico Lenzi