Avvio alla matematica: blocchi e abachi

Un uso appropriato e coordinato dei blocchi aritmetici multibase (BAM) e dell’abaco. In calce il saggio in PDF da scaricare (versione aggiornata, 3 maggio 2011).

L’ingresso nella scuola dell’obbligo determina una rivoluzione fondamentale nel modo di imparare da parte del bambino, poiché l’apprendimento – che per lui sino ad allora è stato spontaneo – si trasforma in parte in apprendimento “imposto”, anche se guidato. Di conseguenza, le difficoltà mnemoniche vengono a svolgere, in chiave negativa, un ruolo determinante. E quelle riguardanti l’apprendimento matematico si fanno maggiormente sentire. Infatti, l’immersione in un mondo pieno di insegne luminose e di cartelloni pubblicitari di ogni tipo rende familiari ai bambini i primi approcci con l’alfabeto e con la scrittura delle parole, anche se circa il 6% di loro ha problemi di lettura e di scrittura. A ciò si deve aggiungere la spinta naturale che essi hanno ad acquisire, attraverso il linguaggio, quello che appare come un mezzo che li avvicina agli adulti, uno strumento essenziale per la “promozione” e la convivenza civile.

Però la stessa cosa non si può dire per la matematica; anche perché una certa cultura attribuisce a questa disciplina un ruolo degno di minor rispetto. Da ciò per gli “addetti ai lavori” deriva il compito di porre particolare attenzione ai primi approcci scolastici con l’aritmetica, onde evitare che qualche difficoltà iniziale possa determinare un atteggiamento di ripulsa e di rigetto nei suoi riguardi.

Tra le prime difficoltà ricordiamo quella legata alla memorizzazione delle cifre della rappresentazione numerica decimale – per la quale rinviamo a [DML] – che possono indurre notevoli problemi di discalculia.

Ai problemi di tipo mnemonico va dedicata una cura tutta particolare; e in quest’ambito un uso appropriato di materiali didattici può aiutare l’alunno a superarli, offrendogli gli strumenti, i tempi e i modi per poterli affrontare con minor affanno. Comunque, va tenuto presente che i primi insegnamenti di tipo “strutturato” in ambito matematico debbono fare i conti con deficit del tutto naturali, legati a una lenta acquisizione del Principio di Conservazione delle quantità, secondo il quale la quantità di una collezione di oggetti non dipende dalla loro collocazione.

Questi deficit – che, secondo i fondamentali studi di Jean Piaget (cf. [PS]), per la maggior parte dei bambini scompaiono intorno ai 6 anni, 6 anni e mezzo – aggiungono difficoltà a difficoltà e rendono problematico l’avvio ai primi elementi di aritmetica; onde l’insegnante dovrà agevolare l’acquisizione del suddetto principio da parte dei suoi allievi.

Acquisizione che, come vedremo, potrà essere verificata e in parte favorita dall’uso dei Blocchi Aritmetici Multibase (BAM) in base due o tre, nonché da altre attività per le quali rimandiamo a [L].

Facciamo presente che, prima dell’introduzione dei BAM, sarà opportuno presentare i primi aspetti della nozione di addizione, intesa come conteggio di palline, caramelle, ecc., collocate in un unico cestino (o in altro contenitore) dopo essere state distribuite – e contate! – in due cestini differenti.

L’accertamento da parte dell’insegnante dell’acquisizione del concetto di addizione nei suddetti termini assicurerà che lo scolaro ha compreso – o è avviato a comprendere – il Principio di Conservazione delle quantità; il quale assicura che il conteggio complessivo delle palline può avvenire anche lasciandole separate nei due cestini, senza che nulla cambi. Cosicché, conoscendo già il numero di palline contenute in ciascun cestino, per averne il numero totale basterà partire dal numero di palline di uno di questi – che sarà inutile ricontare – e proseguire il conteggio con quelle dell’altro. Per giunta, non importa quale sia il cestino scelto per primo, così si ricava immediatamente la proprietà commutativa dell’addizione.

È chiaro che quando si passerà alla “linea dei numeri”, ciò corrisponderà a partire da uno dei due numeri, svolgendo poi sulla linea una quantità di “passi” corrispondente al secondo numero; onde la somma sarà data dal numero su cui ci si arresta.

Facciamo presente che nella scuola primaria sarà bene evitare gli esercizi inutili che fanno passare da un numero espresso in una base allo stesso espresso in un’altra base; questi potranno essere proposti nella scuola secondaria, purché con motivazioni e semplificazioni adeguate. Ovviamente, sarà sempre opportuno transitare dalla base decimale, ove questa non sia una delle due basi di partenza e di arrivo.

Per quel che riguarda i BAM, intanto sottolineiamo che il loro uso è strettamente legato alla sottrazione ripetuta di un sottraendo costante [la base prescelta!], che porta in modo naturale alla nozione di resto, nel caso specifico rappresentato dai blocchi uguali che non si possono aggregare, poiché sono in numero inferiore alla base. Il che prelude alla successiva nozione di divisione con resto.

Tanto per fissare le idee, la base sia tre e si abbiano 14 cubetti BAM da aggregare in lunghi (da tre). Perciò si avranno (si veda fig. 1) 4 lunghi e 2 cubetti residui; onde – a tempo debito – 4 e 2 esprimeranno rispettivamente il quoziente e il resto della divisione di 14 per 3.

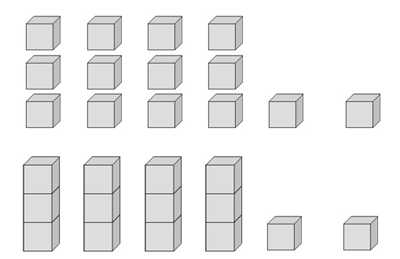
fig. 1

Analogo discorso varrà quando i lunghi saranno aggregati in piatti.

È il caso di notare che i blocchi della base due, costituiti da 2, 4, 8 cubetti (e così via moltiplicando per due) o quelli della base tre, costituiti da 3, 9, 27 cubetti (e così via moltiplicando per tre) sono l’esito di una procedura molto più semplice di quella relativa all’assemblaggio degli euro in riferimento ai vari tagli monetari. Infatti, con gli euro si procede reiterando la sequenza di fattori 2 / 2,5 / 2:

1 € x 2 = 2 €; 2 € x 2,5 = 5 €; 5 € x 2 = 10 €;
10 € x 2 = 20 €; 20 € x 2,5= 50 €; 50 € x 2 = 100 € …

Ma nessuno trova ciò complicato, in quanto ci si abitua presto.

Scarica il PDF con il saggio completo.

Domenico Lenzi