Tiratori di funi

La geometria “delle linee e dei cerchi”, che risale agli antichi agrimensori, gli arpedonapti – tiratori di funi –, deve essere presentata agli alunni come una materia di studio pratica, in cui il racconto, il disegno, la misura, la costruzione, l’uso ordinario delle squadre, del compasso e del goniometro, diventano essenziali nel processo di insegnamento-apprendimento di questa materia.

Quando si entra in classe si avverte quel clima di distacco che molti discenti manifestano nei confronti della geometria, dell’aritmetica e dell’algebra. Durante la mia esperienza come docente di matematica e scienze nella scuola secondaria di primo grado ho avuto modo di conoscere numerosi ragazzi veramente intelligenti che esprimevano però un grande disagio quando venivano posti dinanzi a un problema di geometria o dovevano calcolare il valore di una espressione algebrica.

Molti di loro, nonostante le debolezze evidenziate in matematica, si sono affermati nei vari settori del sociale e della produzione, alcuni sono professionisti, altri bravi artigiani e abili commercianti.

Quando si discute con gli ex alunni, ormai persone adulte, del problema “matematica a scuola”, molti concordano sul fatto che lo studio della matematica, pur essendo utile nelle questioni pratiche e nella vita di tutti i giorni, risultava poco attraente, noioso e difficile.

Del resto è un fatto che i ragazzi, in uscita dalle scuole superiori, prediligono corsi di studio in cui la matematica non c’è oppure è poco rappresentata.

A onor del vero bisogna dire che ci sono alcuni ragazzi che trovano interessante questa importante materia di studio, distinguendosi nel calcolo e, un po’ meno, nella risoluzione dei problemi geometrici.

Per quanto premesso, il vero problema è quello di rendere più interessante, accattivante e piacevole la matematica, attraverso un nuovo modo di presentare e definire gli argomenti di studio.

Cominciamo con il dire, per esempio, che in prima media i libri di testo di geometria si occupano in larga parte degli enti geometrici fondamentali (il punto, la linea, il piano) che i ragazzi percepiscono come entità astratte, lontane dalla loro esperienza e conoscenza diretta.

Gli insegnanti più avveduti, pur facendo riferimento al libro di testo, è bene che introducano la geometria attraverso l’osservazione della realtà vicina alle esperienze dirette dei ragazzi. Lo studio dello spazio tridimensionale, degli oggetti e delle costruzioni che fanno parte dell’ambiente circostante, deve, quindi, precedere lo studio di entità geometriche simboliche e astratte.

La geometria “delle linee e dei cerchi”, che risale agli antichi agrimensori, gli arpedonapti – tiratori di funi –, deve essere presentata agli alunni come una materia di studio pratica, in cui il racconto, il disegno, la misura, la costruzione, l’uso ordinario delle squadre, del compasso e del goniometro, diventano essenziali nel processo di insegnamento-apprendimento di questa materia.

Gli insegnanti facciano in modo che non succeda più che lo studio della geometria a scuola prescinda dall’uso sistematico delle squadre e del compasso e di altri strumenti utili – Geo Gebra, Cabri – per esplorare contesti geometrici significativi.

L’altro giorno, durante l’ora di geometria, i miei alunni, divisi in piccoli gruppi, mi hanno confermato, indirettamente, il loro grande interesse per la geometria: tutti hanno disegnato quadrati, triangoli rettangoli e pentagoni, ritagliandoli dai quadrati, esagoni, usando squadre e compasso, costruendo dal vero un solido sconosciuto, uno “sgorbio” a base esagonale, con facce pentagonali e triangolari. Tutti gli alunni si sono meravigliati, si guardavano increduli, non riuscivano a spiegarsi.

Senza parole, con un gesto, sono stati appaiati, per la base esagonale, due “sgorbi”costruiti nei gruppi, come per magia, i due solidi misteriosi, uniti fra loro, hanno assunto una forma geometrica elegante nota a tutti i ragazzi, il cubo, con una sezione esagonale che toccava con i vertici i punti medi di due spigoli di ogni faccia.

È stata un’ora indimenticabile, magica, i ragazzi mi cercavano per parlarne, per chiedermi alcune particolari proprietà del solido costruito. Tutti gli alunni, nessuno escluso, hanno partecipato all’attività, lavorando nella ricostruzione dell’oggetto misterioso anche a casa. Ci siamo dati appuntamento alla prossima unità oraria per rivivere insieme altri momenti magici!

Riporto qui di seguito l’esperienza vissuta in classe ripresa dalla piattaforma M@t.Abel.

—

Prendete 3 quadrati col lato di 10 cm, tagliateli lungo la linea HK in modo da ottenere 3 triangoli e 3 pentagoni (fig. 1). Disegnate un esagono regolare con i lati lunghi come HK e unite i triangoli e i pentagoni ai lati dell’esagono alternandoli. Provate a chiudere la figura come fosse uno sviluppo. Che tipo di solido avete realizzato? Somiglia a qualche solido che conoscete? Sapete calcolare il volume di questo solido?

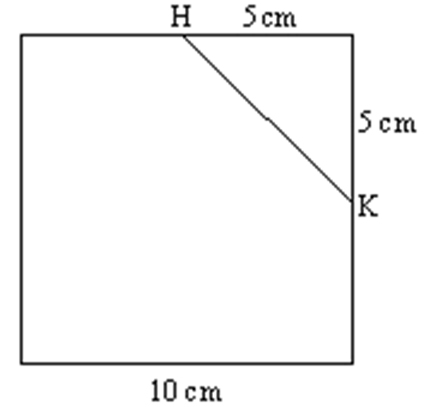
Figura 1

L’insegnante guida gli alunni nella costruzione, che deve essere fatta a piccoli gruppi in modo da avere alla fine più solidi uguali. Terminata la parte operativa, si comincia a descrivere il solido cercando congruenze tra facce e spigoli e somiglianze con altri solidi conosciuti.

Se i ragazzi non lo faranno spontaneamente, l’insegnante a un certo punto chiederà di avvicinare due di questi solidi misteriosi, in modo da far combaciare i due esagoni: si otterrà un cubo. Poco per volta, guidati dall’insegnante, scopriranno che le caratteristiche dello sviluppo disegnato all’inizio corrispondono a quelle che si ritrovano nella sezione: un esagono ottenuto tagliando il cubo per i punti medi di due spigoli di ogni faccia (fig. 2).

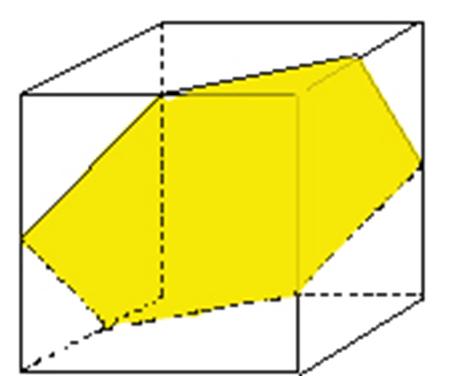
Figura 2

Saverio Fanigliulo